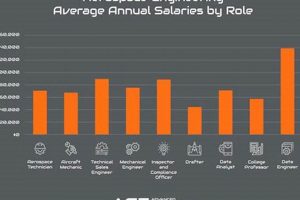
The combination of aerospace engineering principles with advanced mathematical techniques, often accessible in portable document format, represents a critical resource for professionals and students in the field. This readily available material typically encompasses topics such as differential equations, linear algebra, calculus, and numerical analysis, all applied within the specific context of aircraft and spacecraft design, analysis, and operation. For instance, a readily downloadable document might detail the use of computational fluid dynamics (CFD) software, underpinned by sophisticated algorithms, to simulate airflow over a wing profile.
The significance of mathematical proficiency in aerospace engineering is paramount for accurate modeling, simulation, and optimization of complex systems. Benefits include the ability to predict aerodynamic performance, analyze structural integrity, and control flight dynamics. Historically, advancements in aerospace technology have consistently been driven by corresponding developments in mathematical methodologies and their effective implementation. These downloadable resources facilitate access to cutting-edge research, established methodologies, and practical examples, thereby accelerating the pace of innovation within the aerospace sector and enabling a broader audience to engage with these complex subjects.
The subsequent discussion will delve into specific mathematical areas crucial to aerospace engineering, exploring their application in various sub-disciplines. Topics to be covered include orbital mechanics, control systems design, and structural analysis, illustrating how these mathematical tools contribute to solving real-world aerospace challenges.
Tips for Utilizing Aerospace Engineering Mathematics Resources
Maximizing the utility of mathematical resources, often found in portable document format, requires a strategic approach. The following points offer guidance on effectively leveraging these materials for enhanced learning and professional development within the aerospace engineering domain.
Tip 1: Identify Foundational Concepts: Focus initially on mastering core mathematical principles, such as calculus, linear algebra, and differential equations. These fundamentals underpin many advanced aerospace applications. For example, understanding differential equations is essential for analyzing the stability of flight control systems.
Tip 2: Prioritize Application-Oriented Examples: Seek resources that demonstrate the direct application of mathematical concepts to aerospace problems. Case studies involving aircraft design, satellite trajectory calculations, or structural analysis provide valuable context and promote deeper understanding.
Tip 3: Utilize Software Tools for Validation: Employ computational software like MATLAB, Python (with libraries such as NumPy and SciPy), or specialized aerospace tools to validate mathematical models and solutions presented in the documentation. This hands-on approach reinforces theoretical knowledge.
Tip 4: Focus on Numerical Methods for Problem Solving: Aerospace engineering often involves problems that lack analytical solutions. Therefore, proficiency in numerical methods, such as finite element analysis (FEA) or computational fluid dynamics (CFD), is critical. Study resources that detail the algorithms and implementation of these methods.
Tip 5: Cross-Reference Multiple Sources: Consult various available resources to gain a comprehensive perspective on complex topics. Comparing different approaches and explanations can clarify ambiguities and strengthen understanding.
Tip 6: Pay Attention to Dimensional Analysis: In aerospace engineering, dimensional consistency is paramount. Verify that all equations and calculations are dimensionally correct to avoid errors and ensure the validity of results. Examples, as found in the downloadable resources, usually present full dimensional analysis for each application.
Tip 7: Engage with Simulations and Visualizations: Employ simulation software and visualization tools to gain intuitive insights into the behavior of aerospace systems. Visual representations can greatly enhance comprehension of abstract mathematical concepts.
Effectively utilizing these strategies can significantly enhance the understanding and application of complex mathematical concepts in the context of aerospace engineering, as accessible through freely downloadable resources. By focusing on fundamentals, application, validation, and cross-referencing, individuals can maximize their learning outcomes.
The subsequent section will offer insights on specific applications and examples utilizing these methodologies.
1. Analytical Problem Solving
Analytical problem solving forms a cornerstone of aerospace engineering, and resources often found in portable document format provide essential tools and methodologies for its effective application. These documents typically detail mathematical frameworks that enable engineers to dissect complex challenges into manageable components, derive solutions based on established principles, and validate those solutions against real-world constraints.
The presence of analytical methods within aerospace engineering curriculum, often accessible in portable document format, stems from the need for precise calculations in areas like aerodynamics, propulsion, and structural analysis. For instance, determining the lift and drag coefficients of an airfoil requires solving equations derived from fluid dynamics, necessitating a strong foundation in calculus and differential equations. Similarly, designing a stable flight control system involves analyzing its transfer function using Laplace transforms and frequency-domain techniques. Documents detailing such applications underscore the link between mathematical theory and practical problem-solving.
Furthermore, proficiency in analytical problem-solving allows engineers to explore design trade-offs and optimize system performance. By formulating mathematical models and analyzing their behavior, engineers can identify potential weaknesses, refine designs, and improve overall system efficiency. The resources in portable document format often contain example problems and solution strategies that equip individuals with the ability to approach engineering challenges in a structured and analytical way. Ultimately, the effective integration of analytical skills with practical engineering knowledge, as facilitated by these resources, is essential for innovation and advancement in the aerospace field.
2. Computational Fluid Dynamics
Computational Fluid Dynamics (CFD) serves as a crucial component within aerospace engineering, relying extensively on mathematical frameworks often documented in portable document format. These resources provide the theoretical underpinnings and practical implementation details necessary for simulating fluid flow behavior around aerospace vehicles and components.
- Numerical Solution of Navier-Stokes Equations
CFD fundamentally solves the Navier-Stokes equations, a set of nonlinear partial differential equations that describe fluid motion. Resources in portable document format detail various numerical methods like finite volume, finite element, and finite difference methods used to approximate solutions to these equations. The accuracy of these simulations directly impacts the design and performance analysis of aircraft, rockets, and other aerospace structures. For instance, simulating airflow around a wing profile allows engineers to predict lift and drag characteristics, which are essential for aerodynamic optimization. Access to reliable documents detailing these numerical methods ensures the validity and accuracy of the resulting CFD simulations.
- Turbulence Modeling
Turbulent flow, characterized by chaotic and unpredictable motion, is prevalent in many aerospace applications. Accurately modeling turbulence requires sophisticated mathematical models such as k-epsilon, k-omega SST, or Reynolds Stress Models. These models, explained in detail within the resources, introduce additional equations that account for the statistical properties of turbulent flow. The selection of an appropriate turbulence model significantly affects the accuracy of CFD simulations for phenomena like boundary layer separation or jet engine exhaust plumes. A well-documented resource provides the theoretical justification and practical guidance for implementing such models.
- Mesh Generation and Grid Convergence
Before performing a CFD simulation, the physical domain must be discretized into a mesh, representing the geometry numerically. The quality of the mesh significantly affects the accuracy and stability of the simulation. Portable document format resources often cover techniques for generating structured, unstructured, and hybrid meshes. Grid convergence studies, wherein the mesh is refined to assess the sensitivity of the solution to grid size, are essential for ensuring solution accuracy. These studies, supported by mathematical error analysis, are essential for determining the reliability of the CFD results.
- Boundary Conditions and Solver Settings
Defining appropriate boundary conditions is crucial for obtaining accurate CFD solutions. These conditions specify the flow behavior at the boundaries of the computational domain, such as inlet velocity, outlet pressure, or wall temperature. Solver settings, including time step size, convergence criteria, and numerical schemes, also impact the simulation’s accuracy and stability. Portable document format resources provide guidance on selecting appropriate boundary conditions and solver settings based on the specific problem being addressed. Incorrect or poorly chosen settings can lead to inaccurate or unstable simulations.
The aforementioned facets highlight the critical role of mathematical methodologies, often detailed in portable document format resources, in enabling effective and reliable CFD simulations for aerospace applications. These resources empower engineers to perform sophisticated analyses, optimize designs, and ultimately advance the capabilities of aerospace vehicles and systems.
3. Structural Mechanics Analysis
Structural Mechanics Analysis, a critical discipline within aerospace engineering, relies heavily on mathematical principles and methodologies. These principles and methodologies are frequently disseminated through resources in portable document format, which serve as essential tools for engineers involved in the design, analysis, and certification of aerospace structures.
- Finite Element Method (FEM)
The Finite Element Method is a numerical technique for solving complex structural problems. Its implementation involves discretizing a structure into smaller elements, each with its own set of equations that describe its behavior under load. These equations, based on elasticity theory and material properties, are then assembled and solved to determine the overall structural response. Portable document format resources provide detailed explanations of the underlying mathematical formulations, including the derivation of element stiffness matrices, the application of boundary conditions, and the solution of large systems of linear equations. Aircraft wing and fuselage analysis are typical applications of FEM. The use of FEM ensures that an aerospace structure can withstand applied loads without failure.
- Stress and Strain Analysis
Stress and strain analysis are fundamental to understanding the behavior of materials under load. Stress represents the internal forces acting within a material, while strain quantifies the deformation caused by these forces. Portable document format resources detail the mathematical relationships between stress and strain, including Hooke’s Law and constitutive models for various aerospace materials like aluminum alloys, titanium alloys, and composite materials. These resources also explain how to calculate stress concentrations around geometric discontinuities, such as holes or corners, which are critical areas for fatigue analysis. Understanding the distribution of stress and strain helps prevent structural failure.
- Buckling Analysis
Buckling is a phenomenon in which a structure suddenly loses its stability and undergoes large deformations under compressive loads. Buckling analysis involves determining the critical load at which buckling occurs. Portable document format resources present the mathematical equations governing buckling behavior, including Euler’s buckling formula for columns and more advanced models for plates and shells. These resources also explain how to account for imperfections and nonlinear effects that can influence buckling behavior. Buckling is a major concern in aerospace structures, particularly thin-walled components like aircraft fuselages and rocket boosters. This analysis is applied to prevent catastrophic collapse.
- Vibration Analysis
Vibration analysis is essential for ensuring the dynamic stability and performance of aerospace structures. Vibrations can cause fatigue damage, reduce passenger comfort, and interfere with sensitive equipment. Portable document format resources detail the mathematical methods for analyzing structural vibrations, including modal analysis, frequency response analysis, and transient response analysis. These resources explain how to calculate natural frequencies, mode shapes, and damping characteristics of aerospace structures. The analysis is applied to minimize the impacts of vibrations during flight.
These facets of structural mechanics analysis, deeply rooted in mathematical principles and comprehensively documented in portable document format resources, are indispensable for aerospace engineers. They enable the safe and efficient design of aircraft, spacecraft, and related systems by predicting their behavior under various loading conditions and ensuring their structural integrity.
4. Orbital Trajectory Calculation
Orbital trajectory calculation, a fundamental element of aerospace engineering, relies heavily on mathematical formulations and computational techniques, often accessed through resources in portable document format. These downloadable files consolidate complex mathematical models that govern the motion of celestial bodies and spacecraft. The accurate determination of an orbital trajectory, from initial launch to final destination, demands a thorough understanding and application of these mathematical frameworks. Failure to properly apply these principles can lead to mission failure, highlighting the critical significance of this component within the broader field of aerospace engineering mathematics. Real-life examples include the calculation of transfer orbits for interplanetary missions or the precise positioning of communication satellites. The success of these endeavors hinges on the precise application of mathematical models, algorithms, and numerical methods contained within such resources.
These portable document format documents often detail Kepler’s laws of planetary motion, which provide the foundation for understanding orbital mechanics. They also present advanced techniques, such as perturbation theory, which accounts for deviations from ideal Keplerian orbits caused by gravitational influences from other celestial bodies or atmospheric drag. Moreover, numerical integration methods like the Runge-Kutta method, are crucial for accurately propagating orbital trajectories over extended periods. The application of these techniques is exemplified in the calculation of rendezvous maneuvers, where a spacecraft must precisely match its position and velocity with another object in orbit. The accurate execution of such maneuvers depends on rigorous mathematical modeling and simulation.
In conclusion, orbital trajectory calculation constitutes an integral part of the mathematical knowledge base necessary for aerospace engineering. Resources in portable document format provide a consolidated source for understanding the relevant mathematical models, algorithms, and numerical methods. Challenges in this area arise from the inherent complexity of orbital dynamics and the need for high-precision calculations. Nonetheless, mastering the principles of orbital trajectory calculation is crucial for the successful execution of a wide range of space missions and advancements in aerospace technology.
5. Control Systems Design
Control Systems Design within aerospace engineering relies fundamentally on a robust understanding of mathematical principles, often acquired and applied through resources available in portable document format. The design and analysis of stable and effective control systems for aircraft, spacecraft, and related systems necessitate proficiency in several mathematical areas, including linear algebra, differential equations, Laplace transforms, and complex analysis. For example, designing an autopilot system for an aircraft requires formulating a mathematical model of the aircraft’s dynamics, analyzing its stability using techniques like Bode plots and Nyquist criteria, and synthesizing a control law that meets performance specifications such as rise time, settling time, and overshoot. These mathematical techniques and associated examples are often detailed within specific downloadable resources.
Portable document format documents addressing control systems design provide engineers with the tools to model system behavior, predict performance, and mitigate potential instabilities. The mathematical foundations enable engineers to analyze system stability, assess disturbance rejection capabilities, and optimize controller parameters to meet specific mission requirements. Specific examples include the design of attitude control systems for satellites, which requires precise mathematical modeling of the satellite’s inertia and external disturbances, or the design of flight control systems for unmanned aerial vehicles (UAVs), which requires accounting for aerodynamic nonlinearities and sensor noise. Access to these resources empowers engineers to design robust and reliable control systems that ensure safe and effective operation of aerospace vehicles.
In summary, Control Systems Design is an essential aspect of aerospace engineering, deeply intertwined with mathematical principles accessible through portable document format resources. The challenges in this field arise from the inherent complexity of aerospace systems and the stringent performance requirements imposed on control systems. Mastery of these mathematical concepts is crucial for aerospace engineers to design and implement effective control strategies that meet the demanding challenges of modern aerospace applications. Effective control systems provide not only enhanced performance but also ensure safe and reliable operational characteristics.
Frequently Asked Questions Regarding Aerospace Engineering Mathematics Resources in PDF Format
This section addresses common inquiries and misconceptions concerning the application of mathematical principles within aerospace engineering, particularly as they relate to resources available in portable document format. The information provided aims to clarify the scope, utility, and limitations of such resources.
Question 1: What specific mathematical topics are typically covered in resources related to aerospace engineering mathematics in PDF format?
Such resources generally encompass a wide range of mathematical disciplines including calculus, linear algebra, differential equations (ordinary and partial), complex analysis, numerical methods, probability and statistics, and optimization techniques. The emphasis on each topic varies depending on the specific application, but a strong foundation in all listed areas is generally expected.
Question 2: How are these mathematical concepts applied in practical aerospace engineering scenarios?
These mathematical concepts are fundamental to numerous applications within aerospace engineering. Examples include computational fluid dynamics simulations, structural analysis of aircraft components, orbital mechanics calculations for spacecraft trajectories, control systems design for flight stability, and signal processing for radar and communication systems. Numerical methods, in particular, play a crucial role in solving problems that lack analytical solutions.
Question 3: What level of mathematical background is required to effectively utilize these portable document format resources?
A solid foundation in undergraduate-level mathematics is generally necessary to comprehend the material presented in such resources. Some resources may assume prior knowledge of advanced topics, such as tensor analysis or functional analysis, depending on the specific subject matter. It is recommended to review fundamental mathematical concepts before delving into specialized applications.
Question 4: Are resources focusing on aerospace engineering mathematics in PDF format suitable for self-study or formal coursework?
These resources can be valuable for both self-study and as supplementary material for formal coursework. However, it is important to recognize that self-study requires a high degree of self-discipline and the ability to critically evaluate the information presented. For formal coursework, these resources can complement textbooks and lectures, providing additional examples and insights.
Question 5: What are the limitations of relying solely on portable document format resources for learning aerospace engineering mathematics?
While these resources offer convenient access to information, they may lack the interactive learning environment and personalized guidance provided by instructors in a classroom setting. Additionally, some resources may not be peer-reviewed or rigorously vetted, potentially leading to inaccuracies or incomplete explanations. Therefore, it is crucial to exercise caution and critically evaluate the credibility of the information.
Question 6: Where can one find reliable and comprehensive resources pertaining to aerospace engineering mathematics in PDF format?
Reliable resources can often be found on university websites, government research laboratories (e.g., NASA), professional organizations (e.g., AIAA), and reputable online repositories. It is advisable to prioritize resources authored by recognized experts in the field and to verify the accuracy of the information through cross-referencing with other sources. Checking for peer-review status or affiliation with academic institutions can help ensure credibility.
In conclusion, portable document format resources related to aerospace engineering mathematics offer a valuable avenue for acquiring and applying mathematical knowledge within the field. However, it is essential to approach these resources with a critical mindset, a solid mathematical foundation, and an awareness of their inherent limitations.
The following section will provide specific examples of how these resources can be used to address real-world aerospace engineering problems.
Conclusion
The preceding discussion has extensively examined the role of readily available resources concerning “aerospace engineering mathematics pdf.” This examination reveals a vital intersection between advanced mathematical techniques and their practical applications within the aerospace domain. The accessibility of comprehensive documentation, detailed analysis methods, and concrete examples via portable document format significantly contributes to the dissemination of critical knowledge and promotes innovation. These downloadable documents are fundamental to understanding the underlying principles of flight, space exploration, and the design of advanced aerospace systems.
The continued development and responsible use of “aerospace engineering mathematics pdf” resources are crucial for the ongoing advancement of the field. Researchers, engineers, and students are encouraged to rigorously apply these tools, validate theoretical models with experimental data, and contribute to the refinement of existing methodologies. Through collaborative efforts and the judicious application of mathematical principles, the field of aerospace engineering can continue to push the boundaries of exploration and technological innovation.